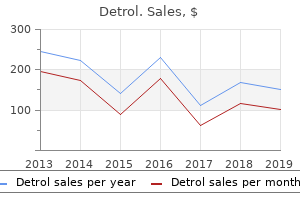
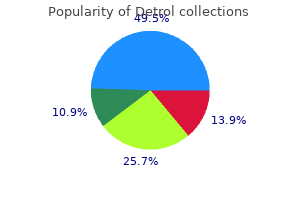
"Order 2mg detrol free shipping, medicine 035".
By: M. Falk, M.A.S., M.D.
Clinical Director, University of North Carolina School of Medicine
The most important is the use of a manometer as a calibration standard for the transducers medicine dropper cheap 1mg detrol overnight delivery. All multitube systems-the manometer medications for adhd trusted detrol 1 mg, the Scanivalve, and the electronic scannermust be phased; that is, the engineer must know which pressure port on the model is connected to which manometer tube, Scanivalve port, or scanner port. After all the model ports are connected and phased, they must be checked for both plugs and leaks. A leak will show as a change in pressure after a pressure is applied to the model pressure 4. If either of these occur and cannot be repaired, that model pressure port must be either eliminated from the data base or effectively marked as defective. This process has been improved greatly by using the computer system directly and interactively to check and record pressure port response and create a corresponding cross-reference table. This process eliminates the requirement to trace a large number of small tubes from ports to transducers and keep track of the corresponding identifying little tags that inevitably are oriented in the most awkward orientations. We assume that a choice of device such as a thermocouple, resistance thermometer, or glass thermometer will be guided by the specific installation requirements in a facility. Here we will mention the basic issues regarding the measurement of temperature in a low-speed flowing stream of air. Similar to the case of pressure, the temperature of a flowing stream is called "static temperature" and is considered a measure of the average random translational kinetic energy of the gas molecules. The temperature will be sensed by an adiabatic probe in thermal equilibrium and at rest with respect to the gas. If observations are made from a frame in which the gas has a nonzero average velocity, then the thermal equivalent of the directed kinetic energy of the gas is termed the "dynamic temperature. The dynamic temperature is conveniently expressed in terms of the Mach number and the ratio of specific heats: the dynamic temperature is not large for subsonic flows but is quite measurable. For T near standard sea level atmospheric conditions it is -1°F for a Mach number of 0. The "total temperature" is the sum of the temperature and the dynamic temperature. The total temperature would be sensed by an idealized probe that "stagnates" an idealized gas. The relation between the total temperature and the temperature in the flowing gas is obtained from the First Law of Thermodynamics and can be expressed as In a real gas the temperature at a stagnation point is not generally equal to the total temperature (see Benedict). However, for air at low Mach number and for pressures not too far different from atmospheric, the difference between "stagnation temperature" and total temperature is very small and can be neglected. In our case, then, the temperature is essentially constant through a boundary layer on the tunnel wall. Thus, an easy method of obtaining stream temperature is through the use of a flush, wall-mounted temperature probe. The probe should be located in the test section in a region where its chance of damage is minimal. The true velocity and viscosity are needed for the calculation of the Reynolds number, the velocity ratio in flutter model testing, to match the advance ratio in propeller power testing and helicopter rotor testing, and so forth. If the temperature probe is located in the settling chamber, then the appropriate correction should be applied to infer the test-section thermodynamic temperature. Pitots with hemispherical noses begin to show errors in total pressure at very low angles of flow inclination. Pitot tubes with a sharp square nose begin to show errors near 8" flow inclination. A Kiel tubela can provide accurate stagnation pressure for flow angles beyond 30". The pitot is pitched or yawed depending on which is more convenient to determine its sensitivity to flow angularity. An excellent discussion of probe methods for measuring fluid velocity is given by Ernrich. The orifice at A senses total head p + lpv2, the orifices at B sense the and static pressure. If the pressures from the two orifices are connected across a manometer or pressure transducer, the pressure differential will be approximately lpv2, from which the velocity may be calculated provided the density is available. The density can be calculated from the equation of state based on a temperature measurement and the static pressure measurement.
For at each stage when one is using a logical system symptoms xxy buy discount detrol 2mg online, there is a very large number of alternative steps keratin smoothing treatment buy discount detrol 1mg on-line, any of which one is permitted to apply, so far as obedience to the rules of the logical system is concerned. These choices make the difference between a brilliant and a footling reasoner, not the difference between a sound and a fallacious one. Propositions leading to imperatives of this kind might be "When Socrates is mentioned, use the syllogism in Barbara" or "If one method has been proved to be quicker than another, do not use the slower method". The explanation of the paradox is that the rules which get changed in the learning process are of a rather less pretentious kind, claiming only an ephemeral validity. This should apply most strongly to the later education of a machine arising from a childmachine of well-tried design (or programme). Most of the programmes which we can put into the machine will result in its doing something that we cannot make sense of at all, or which we regard as completely random behaviour. Intelligent behaviour presumably consists in a departure from the completely disciplined behaviour involved in computation, but a rather slight one, which does not give rise to random behaviour, or to pointless repetitive loops. A random element is rather useful when we are searching for a solution of some problem. The systematic method has the advantage that there may be an enormous block without any solutions in the region which has to be investigated first. Now the learning process may be regarded as a search for a form of behaviour which will satisfy the teacher (or some other criterion). Since there is probably a very large number of satisfactory solutions the random method seems to be better than the systematic. How could one keep track of the different genetical combinations that had been tried, so as to avoid trying them again? We may hope that machines will eventually compete with men in all purely intellectual fields. Many people think that a very abstract activity, like the playing of chess, would be best. Again I do not know what the right answer is, but I think both approaches should be tried. GЁ del, "Uber formal unentscheidbare SЁ tze der Principia Mathematica und verwandter Systeme, I", o a Monatshefte fЁ r Math. Turing, "On Computable Numbers, with an Application to the Entscheidungsproblem", Proc. But if variations useful to any organic being do occur, assuredly individuals thus characterized will have the best chance of being preserved in the struggle for life; and from the strong principle of inheritance they will tend to produce offspring similarly characterized. This principle of preservation, I have called, for the sake of brevity, Natural Selection. It is important to remember that there were entities called computers before Turing came up with his idea but they were people, clerical workers with enough mathematical skill, patience, and pride in their work to generate reliable results of hours and hours of computation, day in and day out. This proposition will be found, on careful examination, to express, in condensed form, the essential purport of the Theory, and to express in a few words all Mr. To this day many people cannot get their heads around the unsettling idea that a purposeless, mindless process can crank away through the eons, generating ever more subtle, efficient and complex organisms without having the slightest whiff of understanding of what it is doing. The Pre-Turing world was one in which computers were people, who had to understand mathematics in order to do their jobs. Turing realised that this was just not necessary: you could take the tasks they performed and squeeze out the last tiny smidgens of understanding, leaving nothing but brute, mechanical actions. Examining the Work and Its Later Impact 571 What Darwin and Turing had both discovered, in their different ways, was the existence of competence without comprehension (Dennett, 2009, from which material in the preceding paragraphs has been drawn, with revisions). This inverted the deeply plausible assumption that comprehension is in fact the source of all advanced competence. Why, after all, do we insist on sending our children to school, and why do we frown on the old-fashioned methods of rote learning? The very idea that mindless mechanicity can generate human-level or divine level!
Buy detrol without a prescription. Anxiety Meaning Social Anxiety Symptoms Anxiety Quiz Sleep Anxiety Sleep Anxiety.
But if the active region is too wide the system no longer approximates the behaviour of a thin ring and one can no longer expect the tentacles to form a single whorl medicine 2410 buy detrol 2mg mastercard. In the case of woodruff the leaves appear in whorls on the stem medications knowledge best order detrol, the number of leaves in a whorl varying considerably, sometimes being as few as five or as many as nine. The numbers in consecutive whorls on the same stem are often equal, but by no means invariably. It is to be presumed that the whorls originate in rings of active tissue in the meristematic area, and that the rings arise at sufficiently great distance to have little influence on one another. The number of leaves in the whorl will presumably be obtainable by the rule given above, viz. Another important example of a structure with polygonal symmetry is provided by young root fibres just breaking out from the parent root. Initially these are almost homogeneous in cross-section, but eventually a ring of fairly evenly spaced spots appear, and these later develop into vascular strands. In this case again the full explanation must be in terms of a two-dimensional or even a three-dimensional problem, although the analysis for the ring is still illuminating. When the cross-section is very large the strands may be in more than one ring, or more or less randomly or hexagonally arranged. The two-dimensional theory (not expounded here) also goes a long way to explain this. For when all species are taken into account one must expect that the diameters of the rings concerned will take on nearly all values within a considerable range, and that neighbouring diameters will be almost equally common. Neighbouring values of the ratio circumferences to wave-length should therefore be more or less equally frequent, and this must mean that neighbouring petal numbers will have much the same frequency. The equilibrium patterns on such a filament will be the same as on a ring, which has been cut at a point where the concentrations of the morphogens are a maximum or a minimum. It should be noticed, however, that the theory will not apply unmodified for filaments immersed in water. Chemical waves on spheres: Gastrulation the treatment of homogeneity breakdown on the surface of a sphere is not much more difficult than in the case of the ring. The theory of spherical harmonics, on which it is based, is not, however, known to many that are not mathematical specialists. Although the essential properties of spherical harmonics that are used are stated below, many readers will prefer to proceed directly to the last paragraph of this section. The anatomical structure concerned in this problem is a hollow sphere of continuous tissue such as a blastula. This latter assumption is merely for the purpose of mathematical simplification; the results are almost exactly similar if it is omitted. As in § 7 there are to be two morphogens, and a, b, c, d, µ, h, k are also to have the same meaning as they did there. The operator 2 will be used here to mean the superficial part of the Laplacian, i. The essential property of a spherical harmonic of degree n is that when the operator 2 is applied to it the effect is the same as multiplication by -n(n + 1)/ 2. The analogy with § 7 throughout will indeed be obvious, though the summation with respect to m does not appear there. The meaning of this summation is that there are a number of different patterns with the same wave-length, which can be superposed with various amplitude factors. It is probable that the forms of various nearly spherical structures, such as radiolarian skeletons, are closely related to these spherical harmonic patterns. The most important application of the theory seems, however, to be to the gastrulation of a blastula. Suppose that the chemical data, including the chemical wave-length, remain constant as the radius of the blastula increases. With these values the system is quite stable so long as the radius is less than about 2. Near this point, however, the harmonics of degree 1 begin to develop and a pattern of form (12. Making use of the facts that P0 (cos) = cos, P1 (cos) = P-1 (cos) = sin, 1 1 1 it is seen that X - h is of the form X - h = A cos + B sin cos + C sin sin, which may also be interpreted as X - h = A cos, (12.
If we fix the sign of u by making its vertical component positive (and equal to m where m is the first parastichy number) medications not to mix discount detrol 2 mg overnight delivery, there is a choice of sign for v and Turing makes the choice in which u medicine uses purchase detrol now. With this sign choice the third parastichy vector must be u - v because u - v < u + v. But while v may have a positive or negative vertical component, the second parastichy numbers n is by definition positive and so the second parastichy vector has vertical component equal to ±n. Thus the parastichy number of the third parastichy vector can be m ± n: the sum or difference of the first two. Change of parastichy numbers as a lattice changes: the hypothesis of geometrical phyllotaxis So far the discussion has been about a single, fixed lattice. Turing develops a system of flow matrices to describe these processes in general, which he uses in his subsequent discussion of optimal packings. But the key idea is captured by observing that these changes in geometry can be thought of simply as smooth deformations of the original lattice. The observation that the third parastichy number must be the sum or difference of the first two is then particularly important when we consider how the first two parastichy numbers must change as the lattice is smoothly changed as they can only change when the third nearest point becomes closer than the second nearest point. Now suppose our lattice at some point has first three parastichy numbers, members of the Fibonacci series (pr-1, pr, pr+1). Under smooth change, the order may change but eventually one of the three may drop out. If pr-1 drops out it must be replaced by a new third parastichy number x satisfying x = pr ± pr+1 = pr-1 or pr+2; if pr+1 drops out it must similarly be replaced by pr-2 or pr+1. So if we could forbid lattice transitions that allowed pr to be dropped, we could ensure that lattices which began as Fibonacci remained Fibonacci. This Hypothesis of Geometrical Phyllotaxis is that the third parastichy number has to be larger or smaller than the first two. If Turing could have demonstrated this he would essentially have solved his Fibonacci Phyllotaxis problem. Exploring the Hypothesis of Geometrical Phyllotaxis the Hypothesis of Geometrical Phyllotaxis (H. Turing found this an unsatisfactory mechanism for a model, perhaps because it provides no mechanism to ensure optimal packing, but he notes (see pp. The second, more relevant pages are in the brief but important Outline of the Development of the Daisy, which gives, among other things, a description of numerical simulations that had already been carried out, and which should produce exactly the kind of smoothly changing lattice to which the H. To do that, he needed a lattice representation, not of spots, but of patterns with lattice symmetry. The standard account of the Turing instability sets up equations for two chemicals describing their mutual reactions and diffusions. For some sets of parameters, the solution to the equation is a homogeneous one, but as the parameters vary that state loses stability and solutions appear which are periodic in space. In one dimension x, this is analysed by plotting the dispersion relation (k) between the growth rate in time t and the wavenumber k of solutions e(k)t+ikx of the linearised equation. For certain classes of equations, this dispersion relation can have a maximum at say k0, and the value of this maximum can be changed from negative to positive by changes in parameters. On a plane, the same reaction diffusion system has no preferred direction, so all possible wavevectors u with modulus near k0 are those which are promoted by the dynamics. Turing proceeds to an elegant representation of these constraints by observing the relationship between them and the lattice symmetry of the pattern. The lattice matrix and inverse lattice First, although, we need another way of representing lattices. If this is an (m, n) lattice with rise in and the first and second principal vectors make angles tan-1 1 and tan-1 1 with the vertical, then the principal parastichy vectors are u1 = (a, b) and u2 = (c, d) with L= a c b d = m1 n2 m n (4. We can transform to these coordinates with (x, z) = (1, 2)L and transform back by inverting and then transpose the lattice matrix L to obtain M= A C B a = c D = b d -1T (4. Fourier representations of functions with lattice symmetries Turing introduced a wholly new dimension into the analysis by considering not merely the lattice points themselves, but functions which have the symmetry of the lattice. This is a natural consequence of thinking of the spots as high-points of a surface generated by a reactiondiffusion system, or from the technique of solving such reactiondiffusion systems in Fourier space. If f (x), arising perhaps from such a reactiondiffusion system, has the symmetry of the lattice, then it is defined, in the lattice coordinates above, by specifying f (1, 2) for 0 1, 2 1 within the parallelogram of the first two principal vectors, and as a periodic function can be represented as a Fourier sum, given in Section 12 as f (1, 2) = m,n Am,n e2i(m1 +n2) (4. So f is entirely determined by (i) the lattice generated by M and (ii) the values of A at those lattice points.

